Sage Math

Wanna automate your math homework?

I thought so – computer algebra systems (CASes) are an astoundingly powerful set of tools for doing all manner of mathematical logic, and SageMath is one of the best!

Think WolframAlpha on steroids: a thousand times more powerful, useful for everything from the most tedious calculus homework to actual cutting-edge research in pure and applied math, physics, numerical analysis, scientific computing, machine learning, everything (even I managed to write a paper which used a CAS extensively).

But using CASes is a bit more of an art than a science – you might have to massage a useful answer out of it. So here’s a short list of cool things you can do with Sage to give you a feel for it!

Examples

Almost any kind of symbolic computation is easy!

sage: P = expand((x - 2)*(6 * x - 5)*(-6*x + x^2 + 2)); P
6*x^4 - 53*x^3 + 124*x^2 - 94*x + 20

sage: factor(P)
(x^2 - 6*x + 2)*(6*x - 5)*(x - 2)

sage: diff(P, x)
24*x^3 - 159*x^2 + 248*x - 94

sage: diff(P, x, x, x)
144*x - 318

sage: integral(72*x^2 - 318*x + 248, x)
24*x^3 - 159*x^2 + 248*x

Sage is based on Python syntax, and taking advantage of Python constructs can give you very powerful tools! For example, here’s the Gram-Schmidt process from Math 18, applied to symbolic vector fields!

# Define the inner product for vectors in R^3
def inner_product(v, w):
    return v.dot_product(w)

# Gram-Schmidt process for vectors in R^3
def gram_schmidt(V, inner_product_func):
    U = []
    for i in range(len(V)):
        u = V[i]
        for j in range(len(U)):
            u -= inner_product_func(V[i], U[j]) / inner_product_func(U[j], U[j]) * U[j]
        U.append(u) # if you want vectors to be normalized, divide by |u| here
    return U

var('x y z')
[x.simplify_full() for x in gram_schmidt([vector([-y, x, 0]), vector([0, -y, z]), vector([z, 0, -x])], inner_product)]

[(-y, x, 0), (-xy^2/(x^2 + y^2), -y^3/(x^2 + y^2), z), (-(x^2y^2z - x^2z^3)/(y^4 + (x^2 + y^2)z^2), -(xy^3z - xyz^3)/(y^4 + (x^2 + y^2)z^2), -(xy^4 - xy^2*z^2)/(y^4 + (x^2 + y^2)*z^2))]

The result here might seem intimidating, or un-helpfully large – but expressions of this size are actually quite manageable, even routine, when you have a computer to do it for you. Doing even a single one of these by hand would be painful – but playing around with Sage can really make a lot of progress.

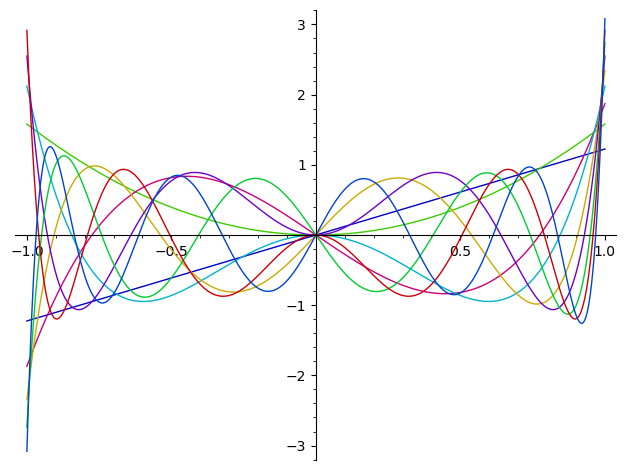
And because this is Python, we could turn this into some numerical code super easily! Better yet, because everything is duck-typed, we can we almost no effort generate the Legendre polynomials from this!

def inner_product(f, g):
    return integrate(f * g, (x, interval[0], interval[1]))

plot(gram_schmidt([x^i for i in range(1, 10)], inner_product))

As one last example, in a problem from my Math 184 homework, I needed to find the coefficient of $x^5$ of the power series of $\frac{\sqrt{1 - \alpha x}}{(1-x)^4}$. Perhaps other tools could have done it without the symbolic $\alpha$, and it’s not immediately obvious how to do it with Sage…. but here’s the trick:

var('alpha')
sage: 1/factorial(5) * diff(sqrt(1 - alpha*x)/(1 - x)^4, x, 5).subs(x = 0)
-7/256*alpha^5 - 5/32*alpha^4 - 5/8*alpha^3 - 5/2*alpha^2 - 35/2*alpha + 56

Differentiating 5 times by hand would be impossible, and while there are cleverer techniques – but Sage doesn’t even skip a beat and just gives you the answer!

Sign me up!

Head over to the SageMath Website to download it, or install the sagemath package from your favorite Linux distro!

And if you want to see more incredible examples, check out the PlanetSage Blog!

Finaly, if you do anything cool with Sage, please share with me (rroychowdhury at ucsd dot edu)!! I’d love to see them!